Rusty Bits: Writing a match-3 calculator in Rust
Motive
A while ago I read an article that mentioned the importance of writing more useless software, just for the sake of knowing how things are done. Inspired by that, I decided to write something that's been on my mind for a while: a match-3 calculator, that games like Bejeweled have to implement in order to function properly.
There's nothing special to it, just a data structure challenge, but one that's quite fun to solve.
TL;DR
I tried three different approaches: A graph based approach, an adjacent matrix approach, but decided to go for the simplest of them all... an array inside an array. Here's the code.
Challenge
Given an 8x8 grid of gems of random colors, identify all the existing matches of 3 elements or more, and also detect if there are possible matches.
For instance:
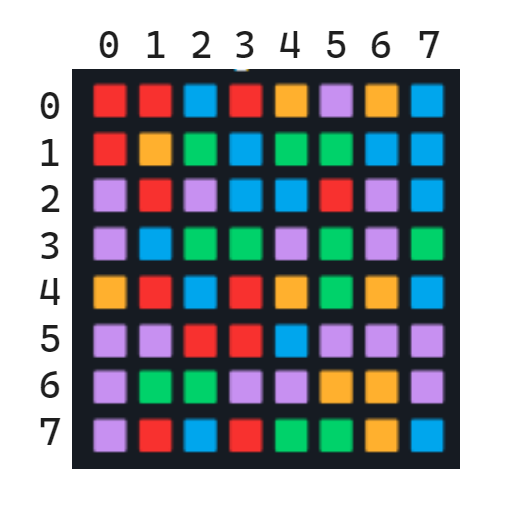
This board has 3 distinct combinations:
Color: ๐ช | Matches: (5, 5)(6, 5)(7, 5)
Color: ๐ช | Matches: (0, 5)(0, 6)(0, 7)
Color: ๐ฆ | Matches: (7, 0)(7, 1)(7, 2)
And also has a couple of possible combinations, for instance, if you moved the green gem on (1, 2) to the right.
Failed attempt #1
For my first attempt I wanted to solve the challenge by holding references to neighboring gems on the gems themselves, and then just traverse through the board counting repeating occurrences, and also measuring possible combinations when actual combinations were not there.
It quickly became uncomfortable to write code like that though, because every gem had four elements wrapped with Option<Rc<RefCell<Cell>>> inside, and simply creating the board and iterating through it to reference every gem proved to be a pain. I ended up abandoning this method right after I managed to generate the random board properly.
Lesson Learned: Initializing an array with indices
After the first attempt, I thought about writing a simple array-based solution, and stumbled upon init_with, a dead simple Rust crate with a very powerful helper: init_with_indices. It allowed me to write code like this:
// At this point, I used to store X and Y coordinates inside gems...
// The final solution does not use this, but it was pretty cool to learn.
Board {
board: <[[Gem; BOARD_SIZE]; BOARD_SIZE]>::init_with_indices(|x| {
<[Gem; BOARD_SIZE]>::init_with_indices(|y| Gem::random(&x, &y))
})
}
I felt that this solution was too simple, and decided to try something more robust (as if it was necessary ๐).
Failed attempt #2
For my second attempt, I thought about using petgraph to generate an adjacency based matrix where Gems would have edges (in my case the weights were a Direction enum) and that way I wouldn't need to worry about all that data wrapping mentioned in the first solution.
Generating the board was really easy, it was just a matter of adding all the nodes, and then all the edges weighed by my Direction enum. I was really happy about it, I had every possible traversal method at hand, nothing could go wrong... right?
Well, it turns out a matrix graph is a REALLY overkill solution for this, and the time it took me to generate the simply 8x8 board was now reaching the milliseconds mark, which was unacceptable for me.
You don't need a rocket launcher to crack an egg
Turns out failing with those overkill solutions was the best thing that could've happened, because I ended up writing a sliding window based solution where I simply run the window through each row of the grid, and then transpose the board and do it again, merging rows where necessary.
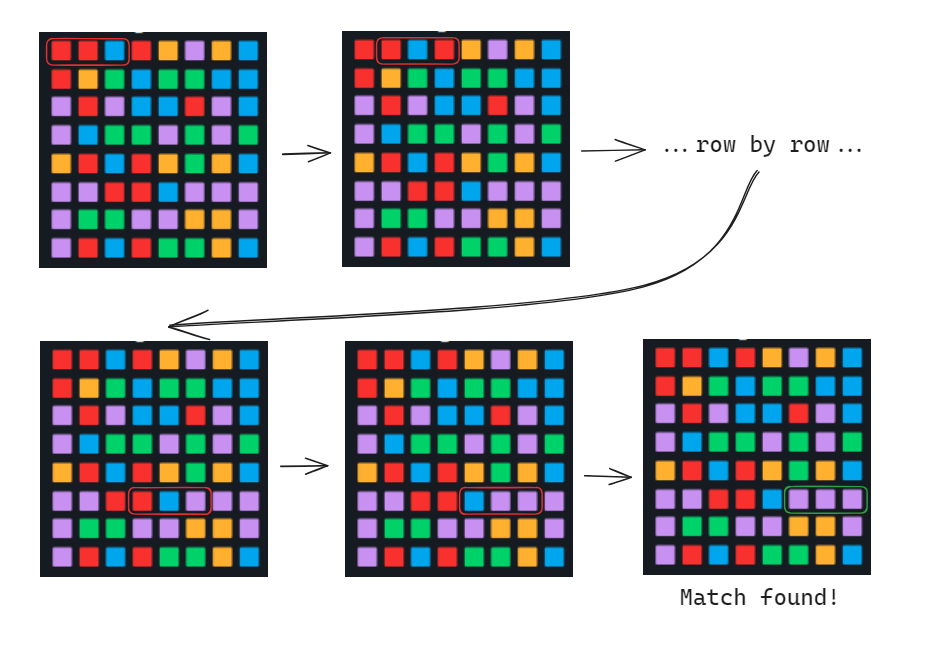
The "main" logic of the code is as simple as this:
fn find_combinations(board: &Board, skip_transposition: bool) -> Vec<GemCombination> {
let mut result: Vec<GemCombination> = vec![];
for (row_num, row) in board.board.iter().enumerate() {
for (starting_col, possible_comb) in row.windows(MIN_COMB_SIZE).enumerate() {
if gems_are_matching(possible_comb) {
result.push(GemCombination::from_match(
possible_comb,
row_num,
starting_col,
skip_transposition,
))
}
}
}
if !skip_transposition {
// Transpose the board and run the same logic.
let transposed_board = board.transpose();
result.append(&mut find_combinations(&transposed_board, true))
}
while contains_mergeable_combinations(&result) {
// Merge colliding combinations
result = sanitize_combinations(result)
}
result
}
The possible match logic is also very similar, and has two different cases:
- Where two identical gems are side-by-side.
- Where two identical gems are separated by a different gem.
For the first case, we simply use sliding windows again, checking wether the surrounding gems of the gems surrounding the duo are of the same color as the duo, like this:
For the second case, we implement a sliding window again with 3 gems, and check if the gem above or under the middle gem matches the same color as the gems on both sides of the window, like so:
Of course, you have to be careful with index bounds, always. ๐
Testing
I wrote a very simple test utility to help me troubleshoot and actually write tests for my code. Remember init_with_indices?
pub fn board_from_string(board_as_string: &str) -> Board {
let rows: Vec<&str> = board_as_string
.split('\n')
.map(|row| row.trim())
.filter(|row| !row.is_empty())
.collect();
Board::from(<[[Gem; BOARD_SIZE]; BOARD_SIZE]>::init_with_indices(|x| {
let row: &str = rows.get(x).unwrap();
let row: Vec<char> = row.chars().collect();
<[Gem; BOARD_SIZE]>::init_with_indices(|y| Gem::new(GemColor::from_char(row[y])))
}))
}
It allows me to write tests like this:
#[test]
fn should_find_four_combinations() {
let board_str = r#"
๐จ๐ฅ๐ช๐ฅ๐จ๐ฉ๐ฉ๐จ
๐จ๐ช๐ฅ๐ฉ๐ฆ๐ฅ๐ฆ๐ฅ
๐ฅ๐ฅ๐ฉ๐ช๐ฆ๐จ๐ฉ๐ช
๐ฅ๐ฆ๐ฆ๐ฆ๐จ๐ฉ๐ฉ๐ฆ
๐ฉ๐ฉ๐ฉ๐ฉ๐ฅ๐ฅ๐ฅ๐จ
๐ฉ๐ฅ๐ฉ๐ฆ๐ฉ๐ฉ๐จ๐จ
๐ฆ๐ฆ๐จ๐จ๐ฆ๐จ๐จ๐ฆ
๐ฆ๐ฆ๐ฅ๐ฆ๐ช๐ฉ๐จ๐จ
"#;
let board = board_from_string(board_str);
assert_eq!(4, board.find_combinations().len())
}
Performance
On average, it scans the board for combinations in around 25.00ยตs, and the possible combination scan really depends on wether it finds a combination early or not. And I'm pretty happy with it ๐.
Conclusion
Doing this challenge helped me pick up the pace to actually build things in Rust just for the sake of getting my hands dirty with it, and I plan to do it more and more as time goes by. Also, I highly recommend Jon Gjengset's Youtube channel as a source of Rust knowledge, I'm learning a ton with his videos, and also feeling inspired to build more complex things.
As always, here's the whole code. I hope you enjoyed the read. ๐ซก